Insertion

RB-INSERT(T, z)
1 y = T.nil
2 x = T.root
3 while x != T.nil
4   y = x
5   if z.key < x.key
6       x = x.left
7   else x = x.right
8   z.p = y
9   if y == T.nil
10      T.root = z
11  elseif z.key < y.key
12      y.left = z
13  else y.right = z
14 z.left = T.nil
15 z.right = T.nil
16 z.color = RED
17 RB-INSERT-FIXUP(T, z)

We can insert a node into an n-node red-black tree in O(lg n) time. To do so, we insert node z into the tree T as if it were an ordinary binary search tree, and then we color z red. To guarantee that the red-black properties are preserved, we then call an auxiliary procedure RB-INSERT-FIXUP to recolor nodes and perform rotations.

RB-INSERT-FIXUP(T, z)
1 while z.p.color == RED
2   if z.p == z.p.p.left
3       y = z.p.p.right
4       if y.color == RED
5           z.p.color = BLACK       // case 1
6           y.color = BLACK         // case 1
7           z.p.p.color = RED       // case 1
8           z = z.p.p               // case 1
9       else if z == z.p.right
10               z = z.p            // case 2
11               LEFT-ROTATE(T, z)  // case 2
12          z.p.color = BLACK       // case 3
13          z.p.p.color = RED       // case 3
14          RIGHT-ROTATE(T, z.p.p)  // case 3
15  else (same as then clause
            with “right” and “left” exchanged)
16 T.root.color = BLACK

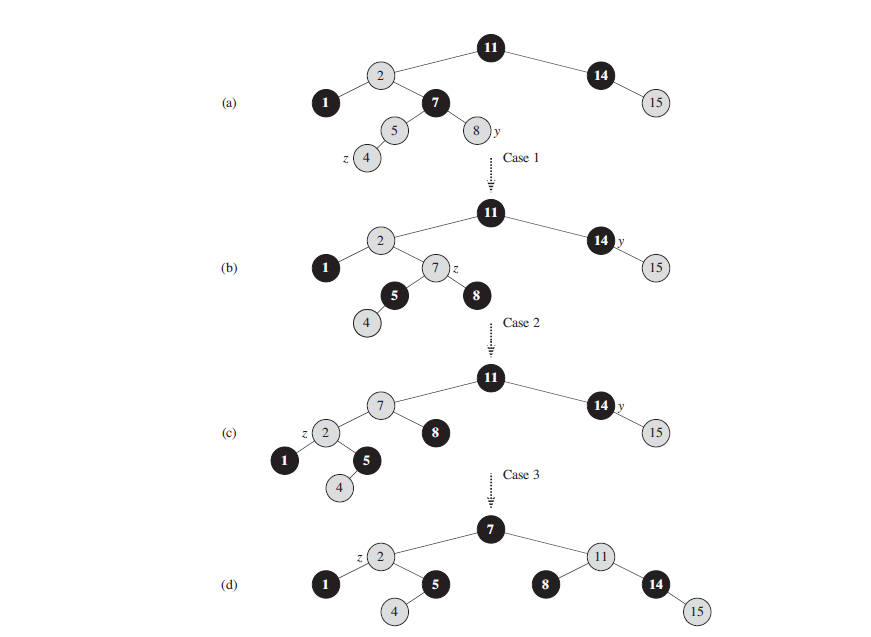
To understand how RB-INSERT-FIXUP works, we shall break our examination of the code into three major steps.

• First, we shall determine what violations of the red-black properties are introduced in RB-INSERT when node z is inserted and colored red.
• Second, we shall examine the overall goal of the while loop in lines 1–15.
• Finally, we shall explore each of the three cases within the while loop’s body and see how they accomplish the goal.

Which of the red-black properties might be violated upon the call to RBINSERT-FIXUP? Property 1 certainly continues to hold, as does property 3, since both children of the newly inserted red node are the sentinel T.nil. Property 5, which says that the number of black nodes is the same on every simple path from a given node, is satisfied as well, because node z replaces the (black) sentinel, and node z is red with sentinel children. Thus, the only properties that might be violated are property 2, which requires the root to be black, and property 4, which says that a red node cannot have a red child. Both possible violations are due to z being colored red. Property 2 is violated if z is the root, and property 4 is violated if z’s parent is red.

The while loop in lines 1–15 maintains the following three-part invariant at the start of each iteration of the loop:

1. Node z is red.
2. If z.p is the root, then z.p is black.
3. If the tree violates any of the red-black properties, then it violates at most one of them, and the violation is of either property 2 or property 4. If the tree violates property 2, it is because z is the root and is red. If the tree violates property 4, it is because both z and z.p are red.

Initialization: Prior to the first iteration of the loop, we started with a red-black tree with no violations, and we added a red node z. We show that each part of the invariant holds at the time RB-INSERT-FIXUP is called:

1. When RB-INSERT-FIXUP is called, z is the red node that was added.
2. If z.p is the root, then z.p started out black and did not change prior to the call of RB-INSERT-FIXUP.

3. We have already seen that properties 1, 3, and 5 hold when RB-INSERTFIXUP is called.

   If the tree violates property 2, then the red root must be the newly added node z, which is the only internal node in the tree. Because the parent and both children of z are the sentinel, which is black, the tree does not also violate property 4. Thus, this violation of property 2 is the only violation of red-black properties in the entire tree.

   If the tree violates property 4, then, because the children of node z are black sentinels and the tree had no other violations prior to z being added, the violation must be because both z and z.p are red. Moreover, the tree violates no other red-black properties.

Termination: When the loop terminates, it does so because z.p is black. (If z is the root, then z.p is the sentinel T.nil, which is black.) Thus, the tree does not violate property 4 at loop termination. By the loop invariant, the only property that might fail to hold is property 2. Line 16 restores this property, too, so that when RB-INSERT-FIXUP terminates, all the red-black properties hold.

Maintenance: We actually need to consider six cases in the while loop, but three of them are symmetric to the other three, depending on whether line 2 determines z’s parent z.p to be a left child or a right child of z’s grandparent z.p.p. We have given the code only for the situation in which z.p is a left child. The node z.p.p exists, since by part (2) of the loop invariant, if z.p is the root, then z.p is black. Since we enter a loop iteration only if z.p is red, we know that z.p cannot be the root. Hence, z.p.p exists.

We distinguish case 1 from cases 2 and 3 by the color of z’s parent’s sibling, or “uncle.” Line 3 makes y point to z’s uncle z.p.p.right, and line 4 tests y’s color. If y is red, then we execute case 1. Otherwise, control passes to cases 2 and 3. In all three cases, z’s grandparent z.p.p is black, since its parent z.p is red, and property 4 is violated only between z and z.p.

Case 1: z’s uncle y is red

Figure 2 shows the situation for case 1 (lines 5–8), which occurs when both z.p and y are red. Because z.p.p is black, we can color both z.p and y black, thereby fixing the problem of z and z.p both being red, and we can color z.p.p red, thereby maintaining property 5. We then repeat the while loop with z.p.p as the new node z. The pointer z moves up two levels in the tree. Now, we show that case 1 maintains the loop invariant at the start of the next iteration. We use z to denote node z in the current iteration, and z’ = z.p.p to denote the node that will be called node z at the test in line 1 upon the next iteration.

1. Because this iteration colors z.p.p red, node z’ is red at the start of the next iteration.
2. The node z’p is z.p.p.p in this iteration, and the color of this node does not change. If this node is the root, it was black prior to this iteration, and it remains black at the start of the next iteration.
3. We have already argued that case 1 maintains property 5, and it does not introduce a violation of properties 1 or 3.

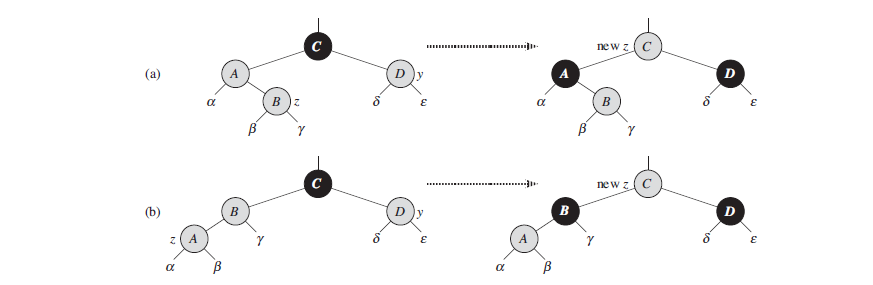
If node z’ is the root at the start of the next iteration, then case 1 corrected the lone violation of property 4 in this iteration. Since z’ is red and it is the root, property 2 becomes the only one that is violated, and this violation is due to z’. If node z’ is not the root at the start of the next iteration, then case 1 has not created a violation of property 2. Case 1 corrected the lone violation of property 4 that existed at the start of this iteration. It then made z’ red and left z’.p alone. If z’.p was black, there is no violation of property 4. If z’.p was red, coloring z’ red created one violation of property 4 between z’ and z’.p.

Case 2: z’s uncle y is black and z is a right child
Case 3: z’s uncle y is black and z is a left child

In cases 2 and 3, the color of z’s uncle y is black. We distinguish the two cases according to whether z is a right or left child of z.p. Lines 10–11 constitute case 2, which is shown in Figure 13.6 together with case 3. In case 2, node z is a right child of its parent. We immediately use a left rotation to transform the situation into case 3 (lines 12–14), in which node z is a left child. Because both z and z.p are red, the rotation affects neither the black-height of nodes nor property 5. Whether we enter case 3 directly or through case 2, z’s uncle y is black, since otherwise we would have executed case 1. Additionally, the node z.p.p exists, since we have argued that this node existed at the time that lines 2 and 3 were executed, and after moving z up one level in line 10 and then down one level in line 11, the identity of z.p.p remains unchanged. In case 3, we execute some color changes and a right rotation, which preserve property 5, and then, since we no longer have two red nodes in a row, we are done. The while loop does not iterate another time, since z.p is now black. We now show that cases 2 and 3 maintain the loop invariant. (As we have just argued, z.p will be black upon the next test in line 1, and the loop body will not execute again.)

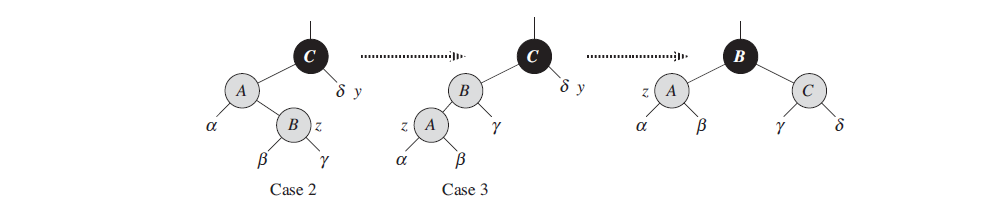
1. Case 2 makes z point to z.p, which is red. No further change to z or its color occurs in cases 2 and 3.
2. Case 3 makes z.p black, so that if z.p is the root at the start of the next iteration, it is black.
3. As in case 1, properties 1, 3, and 5 are maintained in cases 2 and 3. Since node z is not the root in cases 2 and 3, we know that there is no violation of property 2. Cases 2 and 3 do not introduce a violation of property 2, since the only node that is made red becomes a child of a black node by the rotation in case 3. Cases 2 and 3 correct the lone violation of property 4, and they do not introduce another violation.

Having shown that each iteration of the loop maintains the invariant, we have shown that RB-INSERT-FIXUP correctly restores the red-black properties.

Analysis

What is the running time of RB-INSERT? Since the height of a red-black tree on n nodes is O(lg n), lines 1–16 of RB-INSERT take O(lg n) time. In RB-INSERTFIXUP, the while loop repeats only if case 1 occurs, and then the pointer z moves two levels up the tree. The total number of times the while loop can be executed is therefore O(lg n). Thus, RB-INSERT takes a total of O(lg n) time. Moreover, it never performs more than two rotations, since the while loop terminates if case 2 or case 3 is executed.