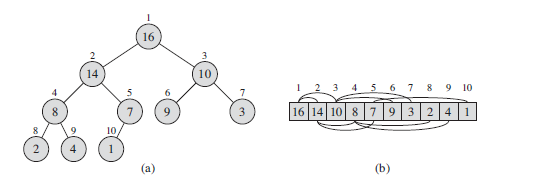
堆排序

堆

（二叉）堆是一个数组，可以被看成是一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且是从左到右填充。表示堆的数组A有两个属性：A.length表示数组的个数，A.heap-size表示数组中目前存储的堆元素个数。

给定一个结点的下标i，可以通过下述伪代码计算得到它的父结点、左孩子和右孩子的下标。

PARENT(i)
1 return i/2

LEFT(i)
1 return 2i

RIGHT(i)
1 return 2i + 1
A Max Heap Sample
A max-heap viewed as (a) a binary tree and (b) an array.

二叉堆可以分为两种形式：最大堆和最小堆。

在最大堆中，最大堆性质是指除了根以外的所有结点i都要满足：A[PARENT(i)] >= A[i], 堆中的最大元素存放在根结点中。

在最小堆中，最小堆性质是指除了根以外的所有结点i都要满足：A[PARENT(i)] <= A[i], 堆中的最小元素存放在根结点中。

  • MAX-HEAPIFY过程：其时间复杂度为O(lgn)，它是维护最大堆性质的关键。
  • BUILD-MAX-HEAP过程：具有线性时间复杂度，功能是从无序的输入数据数组中构造一个最大堆。
  • HEAPSORT过程：其时间复杂度为O(nlgn)，功能是对一个数组进行原址排序。
  • MAX-HEAP-INSERT、HEAD-EXTRACT-MAX、HEAP-INCREASE-KEY和HEAP-MAXIMUM过程：时间复杂度为O(lgn)，功能是利用堆实现一个优先队列。

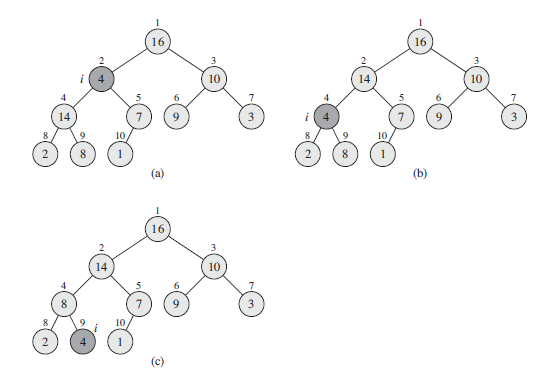
维护一个堆的性质

MAX-HEAPIFY(A, i)
1 l = LEFT(i)
2 r = RIGHT(i)
3 if l <= A.heap-size and A[l] > A[i]
4 	largest = l
5 else largest = i
6 if r <= A.heap-size and A[r] > A[largest]
7 	largest = r
8 if largest != i
9	exchange A[i] with A[largest]
10	MAX-HEAPIFY(A, largest)
A MAX-HEAPIFY Sample
The action of MAX-HEAPIFY(A, 2), where A.heap-size = 10.

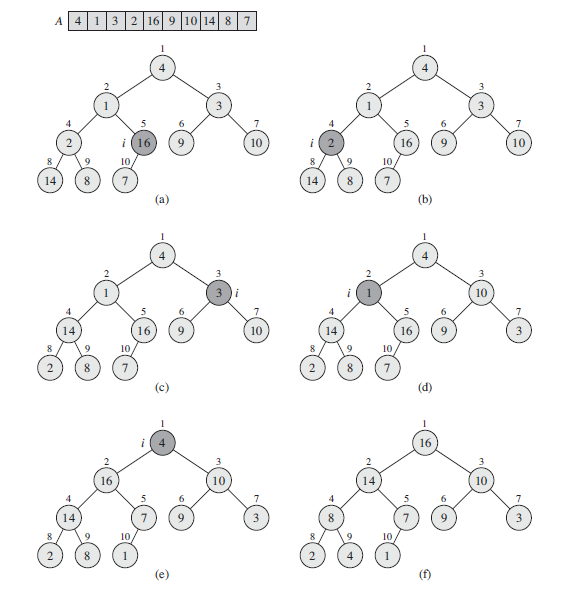
建堆

BUILD-MAX-HEAP(A)
1 A.heap-size = A.length
2 for i = A.length/2 downto 1
3 	MAX-HEAPIFY(A, i)
A BUILD-MAX-HEAP Sample
The operation of BUILD-MAX-HEAP, showing the data structure before the call to MAX-HEAPIFY in line 3 of BUILD-MAX-HEAP.

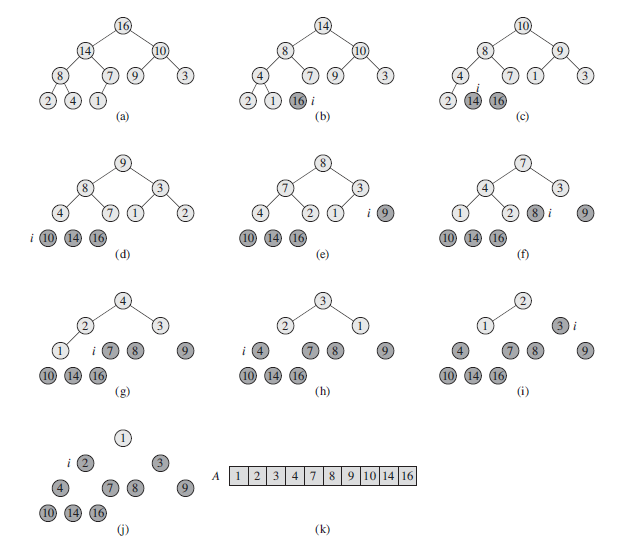
堆排序算法

HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i = A.length downto 2
3   exchange A[1] with A[i]
4   A.heap-size = A.heap-size - 1
5   MAX-HEAPIFY(A, 1)
A HEAPSORT Sample
The operation of HEAPSORT.

优先队列

优先队列(Priority queues)是一种用来维护由一组元素构成的集合S的数据结构，其中的每一个元素都有一个相关的值，称为关键字(key)。一个最大优先队列支持一下操作：

  • INSERT(S, x)： 把元素x插入集合S中。这一操作等价于S = S U {x}。
  • MAXIMUM(S)： 返回S中具有最大键字的元素。
  • EXTRACT-MAX(S)： 去掉并返回S中具有最大键字的元素。
  • INCREASE-KEY(S, x, k)： 将元素x的关键字值增加到k，这里假设k的值不小于x的原关键字值。
EXTRACT-MAX(A)
1 if A.heap-size < 1
2   error “heap underflow”
3 max = A[1]
4 A[1] = A[A.heap-size]
5 A.heap-size = A.heap-size - 1
6 MAX-HEAPIFY(A, 1)
7 return max

HEAP-INCREASE-KEY(A, i, key)
1 if key < A[i]
2   error “new key is smaller than current key”
3 A[i] = key
4 while i > 1 and A[PARENT(i)] < A[i]
5   exchange A[i] with A[PARENT(i)]
6   i = PARENT(i)

MAX-HEAP-INSERT(A, key)
1 A.heap-size = A.heap-size + 1
2 A[A.heap-size] = -∞
3 HEAP-INCREASE-KEY(A, A.heap-size, key)